Super Calculators: The Math of Computers

Introduction

 

Computers touch nearly every area of life in today’s modern world. Calculations carried out on computers have helped cure diseases, ensure our buildings can withstand amazing forces and entertain us with complex computer animations. Of the numerous ways math relates to computers, we will look specifically at three areas of number systems, robotics and computer animation.

 

Number Systems

 

One of the first math skills we master is how to count. Then we learn to manipulate those numbers using various mathematical operations. At the core of a computer is the ability to represent numbers and perform math operations. When we represent numbers we use the digits the 10 symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. We then use a set of rules or an algorithm to express values larger the defined symbols we have. We simply start over at the beginning of the symbols and add a new symbol to the left.

Think of the number 9. When we want to add one more to this quantity we have run out of single symbols to express the new amount. So instead we call it 10. In this way we can think of numbers like an odometer on an old car. When ever the digits for one digit in the number makes a full revolution, the number in the next highest position moves to the next number. Life proceeds as normal and we just think of these symbols as the numbers them selves.

 

But for a computer to keep track of numbers, using 10 distinct symbols or states to represent a number is problematic. You see, in a general sense the computer is just an electrical circuit. A computer needs to represent numbers using only electricity. We could take a voltage and divide it into ten different regions and call each of them our numbers. But it turns out this is really hard and it is much easier, cheaper and faster to represent only two states, 1 and 0. But can we still count to all the numbers? Sure we can, now each wheel on our odometer  will only have two numbers. So we start counting: 0, 1… what now? Well, we apply the same rules we are familiar with. The right most digit rolls around and a new digit is added to the left. Let’s see what happens when we count to 10 in decimal with our new number system.

• 0000 (0)
• 0001 (1)
• 0010 (2)
• 0011 (3)
• 0100 (4)
• 0101 (5)
• 0110 (6)
• 0111 (7)
• 1000 (8)
• 1001 (9)
• 1010 (10)

Well maybe these two digits will work out after all. No writing all of these zeros and ones can get pretty tiring, pretty quickly. There has got to be a way to write things in a more compact form. We could write the numbers as decimal again but then it takes some extra thinking to move things back to binary. What if we could represent each of the 16 patters for four binary numbers using a unique symbol? What would we call 1010? Computer scientists opted to call the number after 9 A. The numbers after A are B,C,D,E,F. Why? Well mostly just because but also because they were familiar symbols that we are used to seeing in ascending order.

Let’s look at the digits that are available in each number system side by side. All of these just give us a symbol to express a value using a set of rules.

The same basic operations we use in decimal can be extended to other number systems. Binary values also open up the possibility of something called Boolean Algebra. Boolean Algebra uses familiar words like AND, OR, NOT and gives them mathematical meaning. As computing evolved important math operations emerged and these were given new names like XOR (Exclusive OR) and NAND (NOT AND) . Lot’s of simple math operations could be chained together to form more complex things like memory and advanced math operations.

 

Robots

 

As the calculating power of computers grows, they are able to perform ever more complex calculations. Advances in computers also helped scientists and engineers find ways to represent more and more of the physical world as electrical signals. Special circuitry can represent electrical signals as numbers. Once information is in the form of a number the computer can do it’s lightning fast math operations to manipulate the data.

Besides being really fast at math, computers can also store information and execute different instructions based on the results of different calculations. A person programs the computer behave in different ways based on calculations they specify. The final piece of the equation that more circuitry can translate numbers into electrical signals.

With these pieces of translating events in the real world to numbers, memory, logical branching and transfer of numbers to the physical world, we start getting a fairly complex system. We can even do something like check for obstacles and move a wheel forward if no obstacles are found. Combine a lot of these feedback loops together and you get what we know today as a robot.

 

Computer Animation

 

When we draw something we draw the shapes and colors we see. If we wanted to draw a scene from a different angle we would draw another picture. How does a computer draw something on the screen? Remember that the computer does not see the world the way we do. It only deals in numbers. So we have to represent the thing to be drawn in numbers. For example, we can use the xyz points on a Cartesian coordinate system.

With points in space we can give further information about which points are connected to one another, colors of regions and other properties like how reflective a surface is. A computer can combine all of this numeric information into a model that it can then use to simulate the behavior of light from different vantage points. This whole process may take millions or billions of calculations to produce the colors that represent a view in space. The computer can save a few calculations and thus time by doing quicker calculations that allow certain calculations to be skipped. For example, we do not need to determine the color for the back side of an object that is not visible.

The advantage of having this information in a model the computer can process is that the computer can repeat the same set of calculations from ANY vantage point in the 3D world. And even though millions and billions of things is a mind boggling amount, modern computers can do millions of calculations each SECOND.

We can go even further and use the computer to simulate physics equations, material behaviors and other complex phenomenon. I dabble in this industry my self, but Tony DeRose from Pixar does good job breaking down specific animation principles using math from Middle School and High School.

 

Conclusion

 

At the core of a computer we find math. If you wish to create new things in technology it will likely also involve math in some way. Simple math operations have been stacked up to form complex systems that can interact with the physical world and make choices based on those inputs. Computers also use math to simulate the physical objects and calculate how light and various forces would interact with that system over time. This only scratches the surface of the wide variety of things math and computers make available.

 

References

• Binary, Hexadecimal and Octal Number Systems, TI Basic Developer http://tibasicdev.wikidot.com/binandhex
• Hour of Code, code.org https://code.org/learn
• Pixar Animation in A Box, Khan Academy https://www.khanacademy.org/partner-content/pixar

Hungry for Math: The Math of Food

 Introduction

 

Imagine you are getting ready for the big game by preparing your delicious dip recipe. Everyone is excited and the guest list is growing by the hour. Your place, with its delicious dip, is the place everyone wants to be. Your recipe is made to serve 8 but now it needs to feed 24. With some simple math you can scale your recipe to meet the demands of your new popularity. Modifying recipes is just one way math can help in the kitchen. In this week’s article we will explore a variety of other ways math impacts our work in the kitchen and the food we eat.

 

 Unexpected Guests

 

Let’s get back to this dip you are making for the big game. While your made from scratch onion dip is known throughout your neighborhood, it is actually a recipe from Food Network’s Alton Brown. (See the references if you actually want to know how to make it) In the time you have been reading this your Aunt Myrtle had some plans fall through and wants to come over for the game and try this delicious dip everyone has been talking about. Aunt Myrtle also wants to bring her bridge club with her. She knows it is a lot of people but promises to pay for any extra supplies needed for such a large group. Now your party is up to 40 people.

You might say well, I have five times as many guests as I planned,  so I can just multiply all of the ingredients by 5. And then you look at the recipe and see that most of the ingredients are expressed as fractions. 1/2 teaspoon of this, 1 and 1/2 cups of that. Fractions can give people trouble well into adulthood so let’s break down what we need to do.

The first thing we need to remember is that any number can be expressed as a fraction. 5 is the same as 5/1.

Second, we can remember some rules for multiplying two fractions. We multiply the numbers on top and that becomes the new top. We multiply the numbers on bottom and it becomes the new bottom.Numbers like 1 and 1/2 we might need to change into a fraction like 3/2 so we can do the same operation on everything.

So 1/2 teaspoon becomes 5/2 teaspoons and 1 and 1/2 cups becomes 15/2 cups. Now these numbers look rather strange. This is because we usually use whole numbers with a remainder when expressing fractions, just like we did with 1 and 1/2 cups earlier. 5/2 teaspoons becomes 2 and 1/2 teaspoons and 15/2 cups becomes 7 and 1/2 cups.

 

Cookie Overload

 

It is the next day after your massive party. Your math skills save the day and let you remain the king of dip. You and your family get a sweet tooth and want to make cookies. You pull out grandma’s old recipe and then you realize the her recipe makes six dozen cookies. That is just way too many cookies for your family of three. So instead of six dozen, three dozen might be more appropriate. (you will have enough to share with your mechanic Marvin and your florist Fern)

Just as we can multiply recipes to make them serve more people, we can also divide them to serve fewer people. As long as the proportion or ratio of each ingredient is the same we can reduce or expand our recipe.

Let’s look at our process again. We’ll express numbers 1 and 1/4 cups sugar as 5/4 cups sugar. We will still multiply, but this time we will multiply by 1/2, which is the same as dividing by 2. We get a new value of 5/8 cups sugar or a little more than half a cup.

 

Clock Work Kitchen

 

After your foray in crazy dip production and  sweet baking success, time passes and you just stick to exact recipes to avoid any extra math in your life. Then Thanksgiving lands in your lap. Aunt Myrtle called again. She will be coming over to celebrate Thanksgiving with you and your family. We are not sure why Aunt Myrtle always insists on inviting her self over, but it works out well for our discussion. Aunt Myrtle lives for tradition and she will expect a turkey with all of the fixings. So you go to the store and buy a 13 pound frozen turkey a week before Thanksgiving. You’ve cooked dip and cookies before, how hard can a turkey be?

Lucky for you, you read the label and see the turkey people say the turkey needs to thaw 24 hours in the refrigerator for every 5 pounds. You realize you’ll have to start prepping for this meal three days before you need to cook it!

As the big day arrives you answer the fifth call this week from Aunt Myrtle. Aunt Myrtle’s last call was to remind you that she doesn’t like the generic brand of cranberry sauce and that dinner should be at 3:00 PM for tradition sake. You look back at the turkey directions and realize the cooking time is based on the size of the turkey. The labels says 20 minutes per pound at 350 degrees Fahrenheit. You get out a pencil. 13 pounds times 20, 260 minutes. There are sixty minutes in an hour so it is going to take 4 hours and 20 minutes for the turkey to cook! You work backwards and you figure out you need to get the turkey in the oven by 10:30 on Thanksgiving morning. You do similar calculations and form a plan for when the potatoes, stuffing and green bean casserole need to go in. The meal is a success and Aunt Myrtle approves of your meal offerings, even if you didn’t have enough sense to get a hair cut before she arrived.

 

One More Slice of Pie

 

You begin to doze on the couch anticipating Aunt Myrtle will soon depart now that dinner has completed. Aunt Myrtle tells you that it is just too dark outside for her to be driving and insists she stay at your house over night. As you prepare the guest room you see that Aunt Myrtle is lugging a suitcase from the trunk of her Cadillac. You start to ponder how convenient it is for her to have an overnight bag with her but decide to let it go.

Later that night your stomach is grumbling so you decide to get another piece of pie. “Who eats dinner at 3:00 PM? 8:30 rolls around and it is like you never ate dinner” you mumble to your self. As you are standing at the fridge enjoying your pie, Aunt Myrtle startles you as you suddenly see her illuminated by the light of the refrigerator.  She is just standing there in her full length night gown and curlers. Then she says to you “More pie? My dear, you are really starting to fill in that sweater. Would you like me to make you a new one?” You pause to process what she said. “Did she really just say that?” you think to yourself. But then you wipe the meringue off your chin and put the drumstick down and ponder her words. While she lacks tact, and general control of her gas, she may have a point. So the next day you start an exercise plan to shed those pounds.

You look up on the internet that one pound of fat equals 3500 calories. You also read that safe weight loss is about 1-2 pounds a week. You cooked a 13 pound turkey, how hard could losing a single pound be? You walk each day in the week for thirty minutes. Some more research tells you that someone your size burns 200 calories by walking for 30 minutes. You multiply it out and figure you burned 1400 calories this week. You were on track with your diet but there was the one time you slipped and ate one brownie, well one ROW of brownies for 500 calories. You run the numbers and find that you only burned an extra 900 calories that week. The amount is not even half a pound. You use your improved math skills to make better choices in the coming weeks and make progress on your goals. With all of this new health surge you even find the energy to paint your house a different color. Aunt Myrtle ends up not being able to find your house for a good six months. Six. Blissful. Months.

 

Conclusion

 

Even if you don’t have an Aunt Myrtle in your life, you can use math to tackle different problems with cooking and food. You can use math to increase the number of servings, decrease the number of servings, plan cooking tasks and to understand the impacts of diet and exercise. Check out the references and videos below to keep learning.

 

 References

 

• Onion Dip From Scratch by Alton Brown http://www.foodnetwork.com/recipes/alton-brown/onion-dip-from-scratch-recipe.html
• Soft and Chewy Chocolate Chip Cookie Recipe http://www.food.com/recipe/soft-and-chewy-chocolate-chip-cookies-48356
• Cooking with Math on Math Central from the University of Regina http://mathcentral.uregina.ca/beyond/articles/Cooking/Cooking1.html
• Real Life Math | Chef http://www.pbslearningmedia.org/resource/mkaet.math.rp.chef/real-life-math-chef/

 

Videos

 

Expensive Dollars: The Math of Money

 Introduction

 

In this installment we are examining the various math topics around money. Now money in general is an extremely broad topic that has a vast amount of theory and entire professions dedicated to different aspects of money (accountants, book keepers, loan officers, bank employees, etc.) Our discussion will focus on basics essential for young people to get a foothold and see a few different simple math uses in action. We’ll cover what money is, income and expenses.

 What is Money?

 

Before we talk about money we should understand what money or currency is. In a general sense, money or currency is made up. But one can touch it and hold it, how can it be made up? Money is made up in the sense that money is merely a social contract that a group has decided on. A value is assigned that maps goods to currency. Once this value is agreed upon, commerce, or an exchange of goods, proceeds from there. You can have commerce without money by simply trading item for item. This is called bartering.

Bartering is simple to visualize. If one person raises chickens and another person raises pigs, they can trade each other. Say the chicken farmer agrees to trade 5 chickens for 1 pig. They make the exchange and enjoy the bounty of their new trade. This works out well because the pig farmer has pigs and wants chickens while the chicken farmer has chickens and wants pigs. This simple system of trading begins to break down under a few different scenarios.

Storage

Pigs have a season. They take a certain amount of time and care before they are ready to sell. After a certain period of time they become extremely large and it takes excessive resources to feed them. Very old pigs may lose their savor and not be as good for consumption. So there is a time frame when it makes sense to sell the pig. But what if the pig farmer does not need chicken at that time? What if no chickens are ready for trade? How does the pig farmer eat chicken when it is not the right time to sell the pigs? The farmers certainly could agree to have a delay in their exchange. An arrangement like: I will give you a pig now for chicken later. They could also make preservation efforts like curing a ham for future sell, etc. But all of these things take time. Money allows the farmers find a buyer during the appropriate season and use currency to purchase things later when they have no goods for sale.

Fractional Amounts

Related to the problem of storage is fractional amounts. What if the chicken farmer can only part with three of his chickens right now? Does the pig farmer give him 3/5 of a pig and keep the rest? In this example this division may actually be possible. The chicken farmer could trade for just the most desirable portions of the pig. But what about the other way around? The pig farmer has only one pig to trade and he needs 2 chickens and some and milk. He might still be able to divide up the cuts of meat but what if the dairy and the chicken farm are far apart and transporting the divided product before it spoils is difficult? Now there are certainly ways around this. The pig farmer could hire a helper (but what would he pay the helper in, pigs too?) or agree to meet at a central place, but things get complicated really fast. Currency can solve this problem by allowing the chicken farmer to transform his goods (chickens) into currency over time. Perhaps the farmer can sell three chickens for $3 now and use $2 from a previous chicken exchange to fund his pig purchase. In the same line of thinking the pig farmer can sell his pig for $5 and pick up chickens when he is that area and milk the next day when he travels to the other part of the region.

No Direct Exchange

Consider a third party who makes lantern oil. Both the pig and chicken farmers need the oil to light their homes. The chicken farmer has chicken to offer for oil and the pig farmer has pigs to offer for oil. But the oil maker isn’t very fond of meat and prefers to eat fresh vegetables. Now they certainly could find another farmer who grows vegetables but things can get complicated. Say the vegetable farmer prefers chicken over pork. The pig farmer could certainly trade a pig for some chickens, chickens for vegetables and vegetables for lantern oil. But this whole exchange takes time to coordinate and execute.  On the other hand, if this area has an agreement on a currency, the pig farmer can sell to an interested buyer for money and buy goods from the lantern oil maker directly. The oil maker can then use the money to buy as many fresh salads as he wants directly from the vegetable farmer.

Desirable Properties of Money

If we can all agree that this piece of paper or that piece of metal has some value, then money or currency is formed. Currency solves a problem by being easy to store, easy to break into pieces and easy to exchange among different parties. But, as we will see, this invention can also introduce different problems like stress and  debt.

Income

 

Now that we have this common form of exchange called money, we need some way to acquire this resource to exchange for things we need and want. Acquiring money is called income. In the most general sense, income is the result of exchanging something you have with someone who wants what you have, for money. Some common things we trade are time, energy, knowledge, and resources.

Time, energy and knowledge are common things people do in jobs to make income. A home owner might pay someone with a lot of strength to dig a ditch. An employer might pay someone to deliver fliers to advertise a business while they stay in the office to handle calls. Another person might get paid to help someone who is injured feel better. There are as many jobs as there are kinds of people.

Our farmers discussed earlier were exchanging resources they had developed over time. A computer chip maker might make a computer part and sell it to interested parties. A person who has a home or property may rent the location (allow others to occupy the space) in exchange for money.As with jobs, there are as many types of resources that can be gathered and exchanged for income as there are kinds of people.

Let’s look at a few different calculations we can do with Income

Wage over Different Time Periods

In the case of a job, some amount of money is exchanged for some result or time. An employer might say a job is $10 an hour and another is $50,000 a year. Translating these numbers between different time frames like $/hour, $/month and $/year can be important for different contexts. Just as we did with our sports discussion, we can use simple math to move from one set of units to another. Some key things to consider:

• While there are 356 days in the year, a person is unlikely to work each and every one of those days. So we need to consider how many days in a given year will be worked.
• The number of hours a person can work is determined by budgets, labor laws and the bounds of human energy. So while there may be 24 hours in a day, you may only be eligible for pay during 8 of them.
• Gross income is different than net income. We will talk about taxes in the expense section, but in short, in most regions there is some amount of money that never hits your pocket. It is taken out in the form of taxes. Net income is how much you actually have at the end of the day.

Moving from an hourly rate to a gross yearly rate looks like the following:

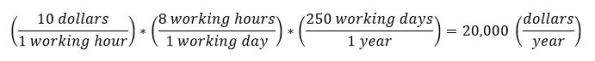
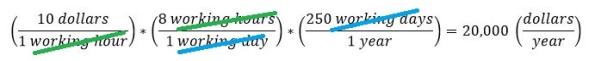
Similarly we can move from from a gross yearly rate to an hourly rate as follows:

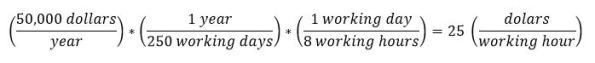
Profit Margin

When goods are sold the seller tries to make a profit. That is to say they wish to bring in more money than they spent to make the item. When the seller spends more money than they bring in that is called a loss. If they neither make money nor lose money it is called a wash. Profits are important because they insulate against future loses. A business or individual who is selling things will often want to calculate how much income they are producing compared to how much they are spending. A profit margin is a ratio of profits to total sales

Let’s consider a girl named Suzie. Suzie 7 years old but she has studied all her life on how to make delicious baked goods. She wants to open a small stand to sell her cookie marvel, Suzie’s Scrumptious Sugar Cookies. Suzie is also a smart business women. She sat down and calculated all of her costs, everything from flour, sugar, to how much gas it takes to run the oven and energy to cool the house after a long day of baking. She estimates each cookie to cost $0.75 to make. She decides to sell each cookie for $1. Her first day goes great and she sells all 100 of the cookies she baked. Let’s calculate her profit margin.

• Suzie spent $75 to make the cookies
• Suzie took in $100 in sales
• Suzie’s net result was $25 in profit

25/100 gives us a value of .25 or 25%. Suzie has a very healthy profit margin of 25%.  A few weeks of good margins like this and Suzie will have the capitol to add new cookies or expand her operations to other neighborhoods.

Importance of Choices

Whatever way one decides to generate income, there are a series of choices that lead up to the options that are available.  Some choices include

• Self Improvement Efforts
• Time management
• Resource Management
• Relationships

Each of these choices may lead to more or less income opportunities. For example, the choice to study a difficult subject while others party may open up many profitable career paths not available to others. Making a good investment might lead to additional income opportunities while a bad or poorly thought out investment might remove income opportunities.

These choices and many more will add together. The following graphic helps to illustrate decisions we can make in what we do with our time:

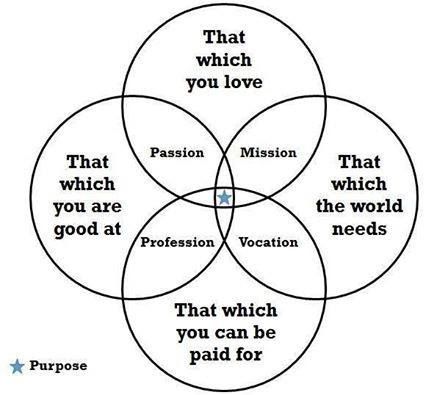
Expenses

 

Expenses are simply money that you have to payout. It might be for a good you need but don’t have, it might be for something you can’t do or it might be part of a social agreement you made. We will limit this discussion to two expenses that might be confusing or new.

Taxes

A tax is an expense required of a person, usually by some larger entity like a city, state or federal government. Taxes are expressed as a percentage of an amount or a fixed value. It might be a percentage of a person’s income, percentage of a sales price or a bridge toll. Taxes are not always called taxes. Sometimes they are called fees, tariffs, duties, tolls, etc. but they mostly behave in a similar way by requiring an expense by some party. Taxes are generally collected with the stated purpose that the individual benefits from some benefit available to all. For example, a person might pay a gas tax when they fill up their car and that tax might be used to build and repair roads. Taxes make a lot of adults pretty heated and there are a lot of active discussions on this topic each day all across the world. People discuss who should be taxed, what should be done with the money, and what amount to tax. This post is not a political post so we we will just talk about the math.

Let’s revisit our two workers from the income section. One made $20,000 a year and the other made $50,000 a year. The United States currently has a variable tax rate that is determined by a complex set of calculations. We’ll leave those complexities to the accountants and just use their gross income without any modifiers to determine a tax from a tax table. We can use these numbers to determine an effective tax rate

If you are still following along, it is important to note these are only federal taxes and there may be many more types of taxes taken on a pay check before it makes it to the earner. Another thing we can do with this is we can revisit the calculations for hourly wage to figure out how much people really make when taxes are factored in:

 

Interest

When discussing interest, it is important to ponder: What do banks sell? An initial response might be that a bank does not sell anything. They just hold your money right? That would not be an accurate observation. A bank collects depositor’s funds and sells them to other people in the form of loans. To say differently, the bank sells money today for more money tomorrow. The increase the bank collects is called interest. Interest can come in the form of a fixed percentage or a value that changes over time.

Simple interest just applies the percentage to the loan. So if you borrowed $1,000 today and agreed to pay 5% simple interest 1 month from now, you would have to pay back $1,050 once the month passes.

Many loans however, do not have simple interest. Instead the interest compounds over time. What this means is that a given interest calculation includes previous interest values. Consider this thought experiment. You start with $1. The you add 10% to that and call it the new value. The you repeat again and again. The first 10 entries would look like:

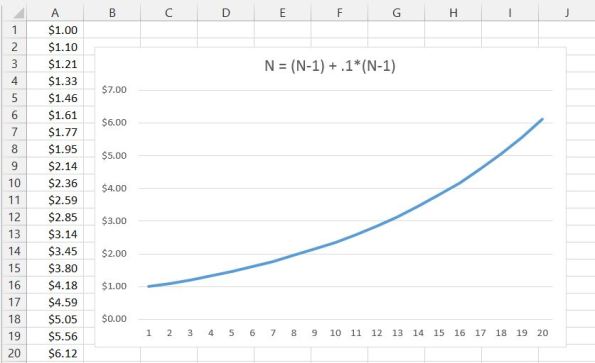
Now let’s look at that over 100 cycles, this time with just the graph:

Imagine for a second that the one dollar in the example was a pack of gum that was put on a credit card. Imagine that credit card had a modest interest rate (for credit cards of 10%) and that the credit card was was forgotten for a little over 8 years. Through compounding interest thousands of dollars would be due. Now this scenario is a bit contrived because a credit card would have a limit and the company would expect payment well before the balance reached this amount, but it does show what compounding interest can do over time.

Speaking of minimum payments, credit card companies will often lure unsuspecting card users with a “minimum payment”. What they do not disclose is that the minimum payment will often be just barely above the interest fee. So each month that goes by the balance is only reduced by a small fraction. This can cause some cards to take up to 30 years to payoff!

Credit lines, such as credit cards are not intrinsically evil. They can be a great help when used appropriately. For example, they can help businesses with cash flow problems who have money but do not have it at the times their debtors need to be paid. Credit can also help with large purchases like cars, houses or education that are important but would otherwise be unobtainable. But the compounding interest of credit cards means that it is very easy to get trapped by the weight of debt. Care must be taken where the terms can be met without spiraling costs.

Loans and complex debt scenarios are often tackled best with the assistance of computers. A computer spread sheet or other software can be configured to evaluate thousands of tedious calculations and determine different outcomes. In the resources section a few different examples are provided for exploration.

 

Conclusion

We can now close our discussion on Money. We learned a little about why currency systems emerged over trading systems. We also learned a little bit about what income is ad a few simple calculations related to hourly wages and profit margins. Finally, we learned about two types of expenses called taxes and interest. In the references below there are more detailed exercises to practice math in these areas.

 

References

• http://ca.pbslearningmedia.org/resource/mkqed-math-rp-creditcards/the-math-of-credit-cards/
• http://www.vertex42.com/Calculators/debt-reduction-calculator.html
• http://debtgraph.jacobgable.com/

 

Videos